rightadvantage.blogg.se - 98 confidence interval z score

98 CONFIDENCE INTERVAL Z SCORE HOW TO
98 CONFIDENCE INTERVAL Z SCORE MOVIE
98 CONFIDENCE INTERVAL Z SCORE PLUS

Using a confidence level of 95, we can use a z-score of 1.96 (see the table below).Start by assigning values to the variables needed for the formula.

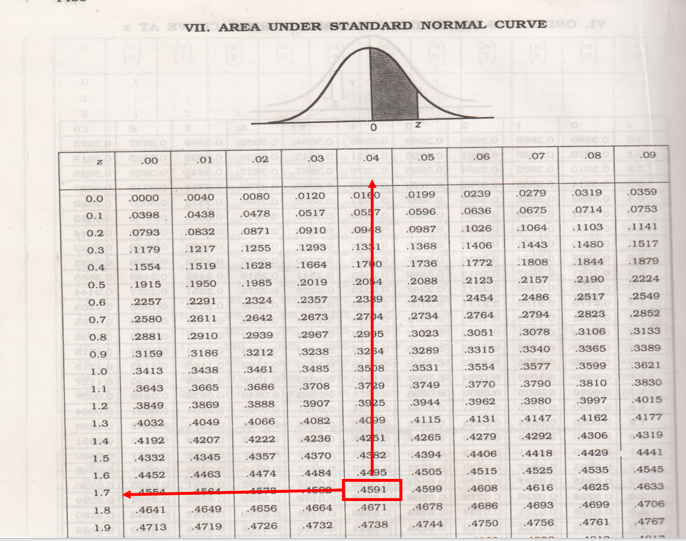
For example, let’s find the confidence interval for a sample with a mean of 14, a standard deviation of 2.5, and a size of 1500. The probability that your interval captures the true population value could be much lower if your survey is biased (e.g. Example: Calculate a 95 Confidence Interval.

A confidence Interval is only related to sampling variability.

If your z-score is between -1.96 and +1.96, your uncorrected p-value will be larger than 0.05, and you cannot reject your null hypothesis because the pattern. The uncorrected p-value associated with a 95 percent confidence level is 0.05. Luckily, this works well in situations where the normal curve is appropriate. The critical z-score values when using a 95 percent confidence level are -1.96 and +1.96 standard deviations.

The standard error calculation involves estimating the true standard deviation by substituting the sample proportion for the population proportion in the formula. For a 99 confidence level, the critical value is approximately 2.58, which is larger than the critical value of 1.96 used in part (a).

Half of 0.98 0.49 Look for this value in the area under Normal curve table.

98 CONFIDENCE INTERVAL Z SCORE HOW TO

Our formula for the confidence interval depends on the normal approximation, so you must check that you have independent trials and a large enough sample to be sure that the normal approximation is appropriate. z - score for 98 confidence interval is 2.33 How to obtain this.If you want more confidence, you will have to settle for a wider interval (bigger z*). is-the-z-score-for-a-98-confidence-interval Confidence Interval Calculator Using. There is a trade-off between the level of confidence and the precision of the interval. 98 percent confidence nterval t score questions Confidence Interval.The margin-of-error being satisfied means that the interval includes the true population value. But, even though the results vary from sample-to-sample, we are "confident" because the margin-of-error would be satisfied for 95% of all samples (with z*=2). Appendix: Critical Values Tables 434 Table A.1: Normal Critical Values for Confidence Levels Confidence Level, C Critical Value, z c 99 2.575 98 2.33 95 1. Each possible sample gives us a different sample proportion and a different interval. To interpret a confidence interval remember that the sample information is random - but there is a pattern to its behavior if we look at all possible samples.

98 CONFIDENCE INTERVAL Z SCORE PLUS

So the data value equals the z-score times the standard deviation, plus the mean. Solving for the data value, x, gives the formula x zsigma + mu. Commonly Used Multipliers Multiplier Number (z*) Since the z-score is the number of standard deviations above the mean, z (x - mu)/sigma. Where z* is a multiplier number that comes form the normal curve and determines the level of confidence (see Table 9.1 for some common multiplier numbers). The Normal Approximation tells us that the distribution of these random errors over all possible samples follows the normal curve with a standard deviation of Sample proportion = population proportion + random error. In Lesson 8 we learned what probability has to say about how close a sample proportion will be to the true population proportion. If you only have the percentile, Z scores are commonly. In other words, a 95 confidence interval comprises all values above the 2.5th percentile and below the 97.5th percentile (1-0.025 0.975).

Therefore, the alpha value has to be split between both sides: 0.05/2 0.025 0.05/2 0.025. We know that estimates arising from surveys like that are random quantities that vary from sample-to-sample. But in our case, the confidence interval is two-sided. Sample is $\bar\right)$.A random sample is gathered to estimate the percentage of American adults who believe that parents should be required to vaccinate their children for diseases like measles, mumps, and rubella.

98 CONFIDENCE INTERVAL Z SCORE MOVIE

Example: A 95% Confidence Interval for Movie Run TimeĪ 95% confidence interval for the mean runtime of Netflix movies is (98, 111).